The statcoulomb (statC) or franklin (Fr) or electrostatic unit of charge (esu) is the physical unit for electrical charge used in the centimetre-gram-second (cgs) electrostatic system of units. The SI system of units uses the coulomb (C) instead. The conversion is
- 1 statC = 0.1 Am/c ≈ 3.33564×10−10 C
The conversion factor (≈ 3.33564×10−10) is equal to 10 divided by the numerical value of the speed of light, c, expressed in cm/s.
In the electrostatic cgs system, electrical charge is a fundamental quantity defined via the electrostatic force (see below); in the SI system, electrical current is fundamental and defined via the electromagnetic force while electrical charge is a derived quantity. The electrostatic system derives the electric charge from Coulomb's law and takes the permittivity as a dimensionless quantity whose value in a vacuum is 1/(4π). Also the use of the permeability of vacuum, 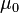 , is avoided, having the consequence that the speed of light appears explicitly in some of the equations interrelating quantities in this system.
, is avoided, having the consequence that the speed of light appears explicitly in some of the equations interrelating quantities in this system.
The statcoulomb is defined as follows: if two objects each carry a charge of 1 statC and are 1 cm apart, they will repel each other with a force of 1 dyne. As a result, in the electrostatic cgs system, Coulomb's law describing the force F between two charges q1 and q2 a distance r apart takes the simple form:

Note that in order for the Coulomb's law formula to work using the electrostatic cgs system, the dimension of electrical charge must be [mass]1/2 [length]3/2 [time]-1. This is different from the dimension of coulombs which accounts for the fact that the factor k mentioned below is not dimensionless.
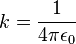
In SI units, the electrostatic constant (where 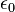 is the permittivity of vacuum) has to be used. Several other laws of electromagnetism also become easier when all quantities are expressed in electrostatic cgs units; this is the main reason that the cgs system of units is still in use in physics and electrical engineering. The main drawback of this approach is that two other sets of cgs units and equations are defined, the electromagnetic and symmetrical systems (the latter system mixes the first two). The equations in all three systems are usually written in non-rationalized form, so-called because the factors 2π or 4π appear often in unexpected places (in situations not involving circular or spherical symmetry, respectively). It is possible, albeit less often done, to write each set of equations in rationalized form.
is the permittivity of vacuum) has to be used. Several other laws of electromagnetism also become easier when all quantities are expressed in electrostatic cgs units; this is the main reason that the cgs system of units is still in use in physics and electrical engineering. The main drawback of this approach is that two other sets of cgs units and equations are defined, the electromagnetic and symmetrical systems (the latter system mixes the first two). The equations in all three systems are usually written in non-rationalized form, so-called because the factors 2π or 4π appear often in unexpected places (in situations not involving circular or spherical symmetry, respectively). It is possible, albeit less often done, to write each set of equations in rationalized form.
The coulomb is an extremely large charge rarely encountered in electrostatics, while the statcoulomb is closer to everyday charges.